5. Rating the quality of evidence
5.1. Introduction
GRADE specifies four quality categories (high, moderate, low, and very low) that are applied to a body of evidence, but not to individual studies. In the context of a systematic review, quality reflects our confidence that the effect estimates are correct. In the context of recommendations, quality reflects our confidence that the effect estimates are adequate to support a particular recommendation.
Guideline panels have to determine the overall quality of evidence across all the critical outcomes essential to a recommendation they make. Guideline panels usually provide a single grade of quality of evidence for every recommendation, but the strength of a recommendation usually depends on evidence regarding not just one, but a number of patient-important outcomes and on the quality of evidence for each of these outcomes.
When determining the overall quality of evidence across outcomes:
- Consider only those outcomes that are deemed critical;
- If the quality of evidence differs across critical outcomes and outcomes point in different directions — towards benefit and towards harm — the lowest quality of evidence for any of the critical outcomes determines the overall quality of evidence;
- If all outcomes point in the same direction — towards either benefit or harm — the highest quality of evidence for a critical outcome, that by itself would suffice to recommend an intervention, determines the overall quality of evidence. However, if the balance of the benefits and harms is uncertain, the grade of the critical outcome with the lowest quality grading should be assigned.
5.1.1. Four levels of evidence
Randomized trials start as high-quality evidence, observational studies as low quality (see table). ‘‘Quality’’ as used in GRADE means more than risk of bias and may also be compromised by imprecision, inconsistency, indirectness of study results, and publication bias. In addition, several factors can increase our confidence in an estimate of effect. This general approach is summarized in the table below.

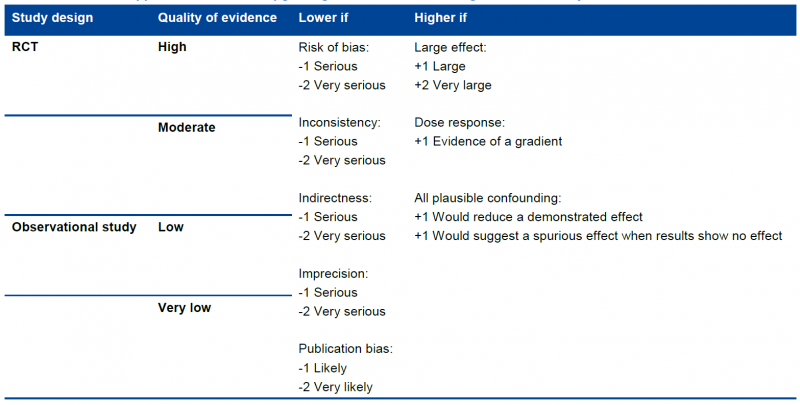
In the following chapters these factors will be discussed in depth. However, it is important to emphasize again that GRADE warns against applying this upgrading and downgrading in a too mechanistic way and to leave room for judgment.
Although GRADE suggests the initial separate consideration of five categories for rating down the quality of evidence and three categories for rating up, with a yes/no decision in each case, the final rating of overall evidence quality occurs in a continuum of confidence in the validity, precision, consistency, and applicability of the estimates. Fundamentally, the assessment of evidence quality remains a subjective process, and GRADE should not be seen as obviating the need for or minimizing the importance of judgment. As repeatedly stressed, the use of GRADE will not guarantee consistency in assessment, whether it is of the quality of evidence or of the strength of recommendation. There will be cases in which competent reviewers will have honest and legitimate disagreement about the interpretation of evidence. In such cases, the merit of GRADE is that it provides a framework that guides one through the critical components of this assessment and an approach to analysis and communication that encourages transparency and an explicit accounting of the judgments involved.
5.1.2. Overall quality of evidence
Guideline panels have to determine the overall quality of evidence across all the critical outcomes essential to a recommendation they make. Guideline panels usually provide a single grade of quality of evidence for every recommendation, but the strength of a recommendation usually depends on evidence regarding not just one, but a number of patient-important outcomes and on the quality of evidence for each of these outcomes.
When determining the overall quality of evidence across outcomes:
- Consider only those outcomes that are deemed critical;
- If the quality of evidence differs across critical outcomes and outcomes point in different directions — towards benefit and towards harm — the lowest quality of evidence for any of the critical outcomes determines the overall quality of evidence;
- All outcomes point in the same direction — towards either benefit or harm — the highest quality of evidence for a critical outcome that by itself would suffice to recommend an intervention determines the overall quality of evidence. However, if the balance of the benefits and downsides is uncertain, then the grade of the critical outcome with the lowest quality grading should be assigned.
5.1.3. GRADE and meta-analysis
GRADE relies on the judgment about our confidence in a (beneficial or adverse) effect of an intervention and therefore it is impossible to apply GRADE correctly if a meta-analysis is not at least considered and the necessary judgments are made on (statistical, methodological and clinical) heterogeneity. It is possible that no pooled effect can or should be calculated if there is evidence of heterogeneity, be it clinical, methodological or merely statistical, but meta-analysis should always be attempted. Otherwise, it is impossible to gather sufficient elements to make the necessary GRADE judgments. Note that heterogeneity is in most cases a reason to downgrade the body of evidence, with some exceptions that will be explained later.
In order to apply GRADE (but actually in order to make a sound judgment on evidence in general) it is essential that at least one person implicated in the development of the guideline understands this guidance and is able to apply it.
GRADE remains rather vague about what to do if only one study is available. We recommend to downgrade the evidence with at least one level, except when the single study is a multicentre study where sample size in the individual centres is sufficient to demonstrate heterogeneity if there is any. Any decision not to downgrade must be explained and justified.
If the primary studies do not allow the calculation of a confidence interval, consider downgrading as judging precision and heterogeneitiy becomes difficult. There are some rare exceptions, when the confidence interval is not needed as all studies point clearly in the same direction. In some cases non-parametric tests are used because the assumption of normality is violated. In these case, the non-parametric measure of uncertainty should be used (most of the time an interquartile range) and interpreted. Decisions taken around these issues should be justified.
5.2. Study limitations, risk of bias
5.2.1. Risk of bias assessment of individual studies should be done using a validated assessment tool
For the quality assessment of individual studies, specific tools were selected by the KCE.
There is no agreed KCE tool for observational studies. At this moment, we limit ourselves to a number of elements that need to be verified when looking at observational studies. There are a large number of assessment tools, but in the scientific community there is considerable disagreement on what items really matter. Moreover, observational studies are way more diverse then RCTs.
Study limitations in observational studies as identified by GRADE are:
- Failure to develop and apply appropriate eligibility criteria (inclusion of control population);
- Under- or overmatching in case-control studies;
- Selection of exposed and unexposed in cohort studies from different populations;
- Flawed measurement of both exposure and outcome;
- Differences in measurement of exposure (e.g., recall bias in case-control studies);
- Differential surveillance for outcome in exposed and unexposed in cohort studies;
- Failure to adequately control confounding;
- Failure of accurate measurement of all known prognostic factors;
- Failure to match for prognostic factors and/or lack of adjustment in statistical analysis;
- Incomplete follow-up.
5.2.2. Moving from individual risk of bias to a judgment about rating down for risk of bias across a body of evidence
Moving from risk of bias criteria for each individual study to a judgment about rating down for risk of bias across a group of studies addressing a particular outcome presents challenges. GRADE suggests the following principles:
- First, in deciding on the overall quality of evidence, one does not average across studies (for instance if some studies have no serious limitations, some serious limitations, and some very serious limitations, one does not automatically rate quality down by one level because of an average rating of serious limitations). Rather, judicious consideration of the contribution of each study, with a general guide to focus on the high-quality studies, is warranted.
- Second, this judicious consideration requires evaluating the extent to which each trial contributes toward the estimate of magnitude of effect. This contribution will usually reflect study sample size and number of outcome events: larger trials with many events will contribute more, much larger trials with many more events will contribute much more.
- Third, one should be conservative in the judgment of rating down. That is, one should be confident that there is substantial risk of bias across most of the body of available evidence before one rates down for risk of bias.
- Fourth, the risk of bias should be considered in the context of other limitations. If, for instance, reviewers find themselves in a close-call situation with respect to two quality issues (risk of bias and, e.g. precision), we suggest rating down for at least one of the two.
- Fifth, notwithstanding the first four principles, reviewers will face close-call situations. They should both acknowledge that they are in such a situation, make it explicit why they think this is the case, and make the reasons for their ultimate judgment apparent.
This approach is summarized in the table below.

5.3. Inconsistency
Widely differing estimates of the treatment effect (i.e. heterogeneity or variability in results) across studies suggest true differences in underlying treatment effect. When heterogeneity exists, but investigators fail to identify a plausible explanation, the quality of evidence should be downgraded by one or two levels, depending on the magnitude of the inconsistency in the results.
Inconsistency may arise from differences in:
- Populations (e.g. drugs may have larger relative effects in sicker populations);
- Interventions (e.g. larger effects with higher drug doses);
- Outcomes (e.g. diminishing treatment effect with time).
Guideline panels or authors of systematic reviews should also consider the extent to which they are uncertain about the underlying effect due to the inconsistency in results and they may downgrade the quality rating by one or even two levels.
GRADE suggests rating down the quality of evidence if large inconsistency (heterogeneity) in study results remains after exploration of a priori hypotheses that might explain heterogeneity.
5.3.1. Heterogeneity and inconsistency
GRADE uses inconsistency and heterogeneity rather interchangeably. However, there are some important nuances:
- A heterogeneity in effect – where it can be assumed that it is randomly distributed – may be due to random variation in the effect amongst studies. To properly address this, the pooled effect should be calculated using random modelling (RevMan uses the DerSimonian and Laird random effects model, but other techniques, such as Bayesian and maximum likelihood, are often used as well). An important condition for the use of these techniques is that it must be plausible that the heterogeneous effect is randomly distributed, which is not always easy to verify. DerSimonian, Laird and maximum likelihood methods have an additional assumption that the effect is normally distributed, while with Bayesian techniques another distribution can be used as well. The studies in this case cannot be considered as inconsistent, and the heterogeneity is accounted for here by the larger confidence interval, so no downgrading is needed here. Note that if the heterogeneity statistic Q is less than or equal to its degrees of freedom (so if I² = 0), DerSimonian gives results that are numerically identical to the (non random effects) inverse variance method.
- If heterogeneity is important for one reason or another, but all estimates point in the same direction, e.g. a strong or very strong effect of the intervention, then one should not necessary downgrade for inconsistency but make a judgement on the plausibility of the study results.
5.3.2. Judging heterogeneity and inconsistency
Exploring and judging heterogeneity is probably the most difficult part in performing and judging a meta-analysis. A number of rules are presented, but a full explanation can be found in the Cochrane Handbook (chapters 9.5 and 9.6). A KCE expert exploring and judging heterogeneity should at least have a good understanding of and ability to apply this Cochrane guidance. If not, he/she should ask for help from somebody who does.
GRADE identifies four criteria for assessing inconsistency in results, and reviewers should consider rating down for inconsistency when:
- Point estimates vary widely across studies;
- Confidence intervals (CIs) show minimal or no overlap;
- The statistical test for heterogeneity which tests the null hypothesis that all studies in a meta-analysis have the same underlying magnitude of effect shows a low p-value;
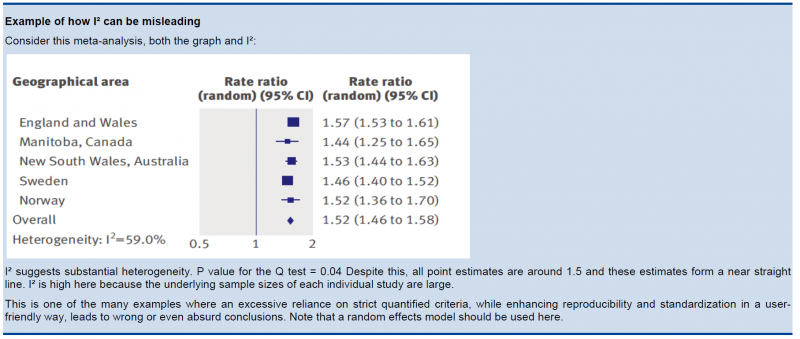
- The I², which quantifies the proportion of the variation in point estimates due to between-study differences, is large
In the past, rigid criteria were used to judge heterogeneity, e.g. an I² of 50% used to be a common threshold. This improves the consistency in judgments, but one risks to be consistently wrong. All statistical approaches have their limitations, and their results should be seen in the context of a subjective examination of the variability in point estimates and the overlap in CIs. So again, transparent judgments are essential here.
What is a large I²? One set of criteria would say that an I² of less than 40% is low, 30 to 60% may be moderate, 50 to 90% may be substantial, and 75 to 100% is considerable. Note the overlapping ranges and the equivocation (‘‘may be’’): an implicit acknowledgment that the thresholds are both arbitrary and uncertain. When individual study sample sizes are small, point estimates may vary substantially, but because variation may be explained by chance, I² may be low. Conversely, when study sample size is large, a relatively small difference in point estimates can yield a large I².
5.3.3. Other considerations
- Risk differences (i.e. absolute risk reductions) in subpopulations tend to vary widely. Relative risk (RR) reductions, on the other hand, tend to be similar across subgroups, even if subgroups have substantial differences in baseline risk. GRADE considers the issue of difference in absolute effect in subgroups of patients, much more common than differences in relative effect, as a separate issue. When easily identifiable patient characteristics confidently permit classifying patients into subpopulations at appreciably different risk, absolute differences in outcome between intervention and control groups will differ substantially between these subpopulations. This may well warrant differences in recommendations across subpopulations.
- Rate down for inconsistency, not up for consistency.
- Even when there is heterogeneity in effect, one must evaluate if the heterogeneity affects your judgment on clinical effectiveness, e.g. when there are large differences in the effect size, but when the estimations point to the same direction (all beneficial or all harmful).
- Reviewers should combine results only if – across the range of patients, interventions, and outcomes considered – it is plausible that the underlying magnitude of treatment effect is similar. This decision is a matter of judgment. Magnitude of intervention effects may differ across studies, due to the population (e.g. disease severity), the interventions (e.g. doses, co-interventions, comparison of interventions), the outcomes (e.g. duration of follow-up), or the study methods (e.g. randomized trials with higher and lower risk of bias). If one of the first three categories provides the explanation, review authors should offer different estimates across patient groups, interventions, or outcomes. Guideline panelists are then likely to offer different recommendations for different patient groups and interventions. If study methods provide a compelling explanation for differences in results between studies, then authors should consider focusing on effect estimates from studies with a lower risk of bias.
Beware of subgroup analyses. The warning below originates from the Cochrane Handbook (chapter 9.6). When confronted with this, consult at least a second opinion of a knowledgeable person.
Subgroup analyses involve splitting all the participant data into subgroups, often so as to make comparisons between them. Subgroup analyses may be done for subsets of participants (such as males and females), or for subsets of studies (such as different geographical locations). Subgroup analyses may be done as a means of investigating heterogeneous results, or to answer specific questions about particular patient groups, types of intervention or types of study. Findings from multiple subgroup analyses may be misleading. Subgroup analyses are observational by nature and are not based on randomized comparisons (an exception is when randomisation is stratified within these subgroups). False negative and false positive significance tests increase in likelihood rapidly as more subgroup analyses are performed (this is due to the multiple testing problem: if you perform a significant test frequently enough, you are likely to find by chance a statistically significant result). If findings are presented as definitive conclusions, there is clearly a risk of patients being denied an effective intervention or treated with an ineffective (or even harmful) intervention. Subgroup analyses can also generate misleading recommendations about directions for future research that, if followed, would waste scarce resources.
5.4. Indirectness
Direct evidence comes from research that directly compares the interventions in which we are interested when applied to the populations in which we are interested and measures outcomes important to patients. Evidence can be indirect in one of four ways:
- First, patients may differ from those of interest (the term applicability is often used for this form of indirectness).
- Secondly, the intervention tested may differ from the intervention of interest. Decisions regarding indirectness of patients and interventions depend on an understanding of whether biological or social factors are sufficiently different that one might expect substantial differences in the magnitude of effect.
- Thirdly, outcomes may differ from those of primary interest, for instance, surrogate outcomes that are not themselves important, but measured in the presumption that changes in the surrogate reflect changes in an outcome important to patients.
- A fourth type of indirectness, conceptually different from the first three, occurs when clinicians must choose between interventions that have not been tested in head-to-head comparisons. Making comparisons between treatments under these circumstances requires specific statistical methods and will be rated down in quality one or two levels depending on the extent of differences between the patient populations, co-interventions, measurements of the outcome, and the methods of the trials of the candidate interventions.
5.5. Imprecision
GRADE suggests that examination of 95% confidence intervals (CIs) provides the optimal primary approach to decisions regarding imprecision. Results are considered imprecise when studies include relatively few patients and few events and thus have wide confidence intervals around the estimate of the effect. In this case a guideline panel will judge the quality of the evidence lower than it otherwise would because of resulting uncertainty in the results.
As a general principle GRADE recommends to consider the rating down for imprecision If a recommendation or clinical course of action would differ if the upper versus the lower boundary of the CI represented the truth. In order to judge this the clinical decision threshold needs to be defined. We explain the situation for both categorical and continuous outcomes.
5.5.1. Clinical decision threshold and minimally important difference
5.5.1.1. Categorical outcomes
As we explained before, it is good to discuss the clinical decision threshold and try to determine them on beforehand. However, one must be careful not to apply this in a too mechanical way, as you need also to take into account the downsides of the intervention, such as side effect or morbidity induced by the intervention, on which in a lot of cases you have only information after collecting the evidence. If it is not possible to determine a threshold, then GRADE suggests to use a RRR or RRI greater than 25%. This 25% threshold is a good and pragmatic starting point, but other factors should be taken into account as well, such as the absolute risk reduction.
5.5.1.2. Continuous outcomes
If the 95%CI upper or lower CI crosses the minimally important difference (MID), either for benefit of harm.
Note: if the MID is not known or the use of different outcome measures required calculation of an effect size, we suggest downgrading if the upper or lower CI crosses an effect size of 0.5 in either direction.
Effect size (ES):
A generic term for the estimate of effect of treatment for a study. Sometimes, the term is used to refer to the standardized mean difference, the difference between two estimated means divided by an estimate of the standard deviation.
To facilitate the understanding we suggest an interpretation of the effect size offered by Cohen, also known as ‘Cohen’s d’[1]. According to this interpretation, an effect size or SMD of around:
- 0.2 is considered a small effect;
- 0.5 is considered a moderate effect;
- 0.8 or higher is considered a large effect.
There are also other methods to standardise effect sizes, such as Glass ∆ or hedges d, depending on the choice of the estimator of the standard deviation.
[1] (Cohen J. Statistical Power Analysis for the Behavioral Sciences. 2nd ed; 1988).
5.5.2. Application and examples
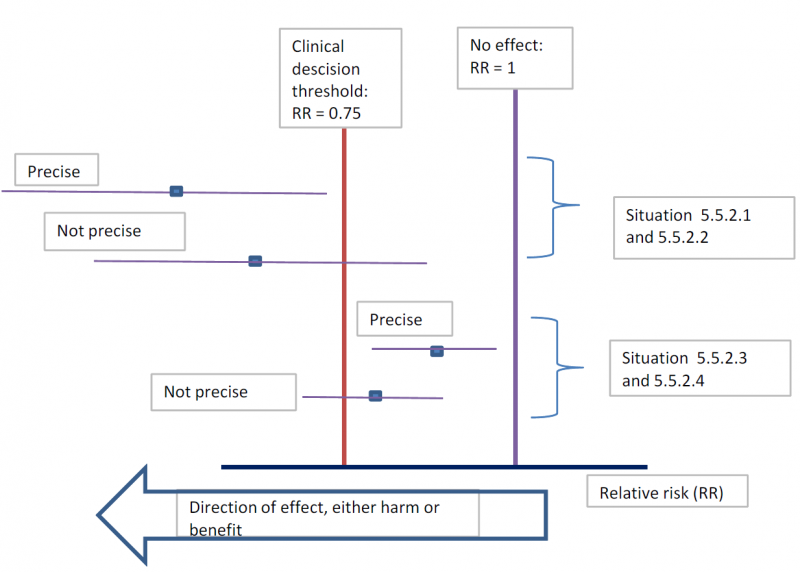
The concrete application of these rules differs according to the situation. Note that imprecision is judged on all outcomes that are judged critical, so the precision of the estimations of the effects on both harms and benefits need to be evaluated.
- Studies indicate a benefit compared to the alternative so you consider recommending the intervention based on the fact that it is beneficial in a clinically significant way.
In this case you must prove not only that the pooled or best estimate of the effect is different from no effect but that it is better than the clinical decision threshold. So the confidence interval must exclude this threshold.
- Studies indicate a harm compared to the alternative so you consider not recommending the intervention based on the fact that it is harmful in a clinically significant way.
In this case you must prove not only that the pooled or best estimate of the effect is different from no effect but that it is more harmful then the clinical decision threshold. So the confidence interval must exclude this threshold.
- Studies indicate that it is not better than the alternative so you consider not recommending the intervention based on the fact that it is not better in a clinically significant way.
In this case you must prove that the pooled or best estimate of the effect is lower that the clinical decision threshold. So the confidence interval must exclude this threshold.
- Studies indicate that it is not more harmful than the alternative so you consider recommending the intervention based on the fact that it is not more harmful in a clinically significant way.
In this case you must prove that the pooled or best estimate of the effect is lower that the clinical decision threshold. So the confidence interval must exclude this threshold.
The last two situations amount to proving non superiority or non inferiority. If the line of no effect is crossed, this does not play a major role in the decision.
5.5.3. Relative versus absolute reductions
The recommended output of a meta-analysis is a relative risk or odds ratio as they are more stable across different baseline risks, but absolute reductions are more useful for clinical decisions. The valid way of estimating the absolute risk reduction is to multiply the relative risk from the meta-analysis with the most plausible estimate or range of estimates of the baseline risk, this is the risk in the assumed control group, often called the assumed control risk.
Assumed control risk (ACR):
As relative risks are more stable, absolute risk reductions are best calculated applying a relative risk reduction to an assumed control risk. Determining the assumed control risk is not always easy and straightforward. The best estimates usually come from Belgian data, e.g. for cancer the data from the cancer registry are a valuable tool. When not available one can use expert opinion or take the baseline effect from studies in the literature. When different studies exist with varying baseline risk sometimes the median control risk is taken (this is what GRADE pro does by default), but it may be better to report a range of plausible values.
5.5.4. Dealing with fragility: Optimal Information Size (OIS)
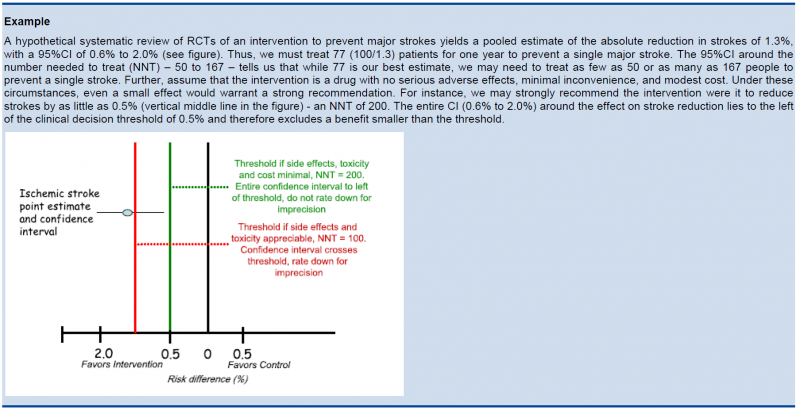
The clinical decision threshold criterion is not completely sufficient to deal with issues of precision. The reason is that confidence intervals may appear narrow, but small numbers of events may render the results fragile.

The reasoning above suggests the need for, in addition to CIs, another criterion for adequate precision. GRADE suggests the following: if the total number of patients included in a systematic review is less than the number of patients generated by a conventional sample size calculation for a single adequately powered trial, consider the rating down for imprecision. Authors have referred to this threshold as the “optimal information size” (OIS). Many online calculators for sample size calculation are available, you can find one simple one at http://www.stat.ubc.ca/∼rollin/stats/ssize/b2.html.
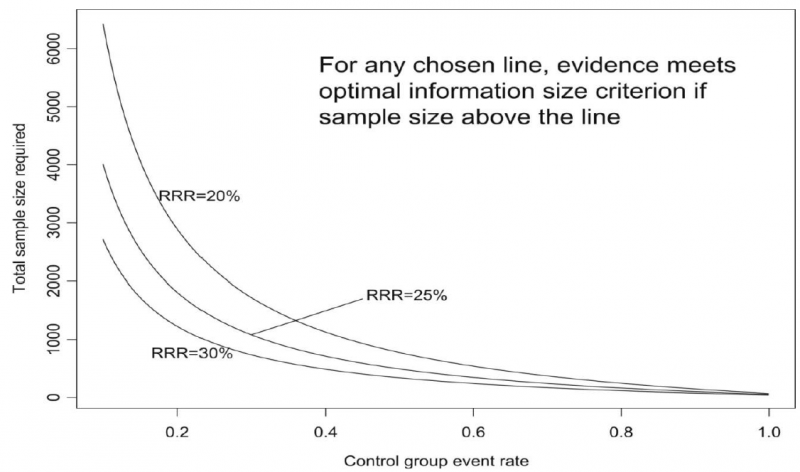
As an alternative to calculating the OIS, review and guideline authors can also consult a figure to determine the OIS. The figure presents the required sample size (assuming α of 0.05, and β of 0.2) for RRR of 20%, 25%, and 30% across varying control event rates. For example, if the best estimate of control event rate was 0.2 and one specifies an RRR of 25%, the OIS is approximately 2 000 patients.
The choice of RRR is a matter of judgment. The GRADE handbook suggested using RRRs of 20% to 30% for calculating the OIS, but there may be instances in which compelling prior information would suggest choosing a larger value for the RRR for the OIS calculation.
Beware, however, not to base your sample size on the RRR of minimally clinical importance, a practice that is suitable for sample size calculations when you set up studies, but not for judging fragility, because it leads to paradoxes: if expected effects are considerably larger than what is clinically important because the clinically important effect is small (e.g. a small effect on mortality in children would be considered important), you would risk to downgrade without good reasons because the required sample size would be too large. Note that the OIS helps judging the stability of the CIs, and not if the study was large enough to detect a difference.
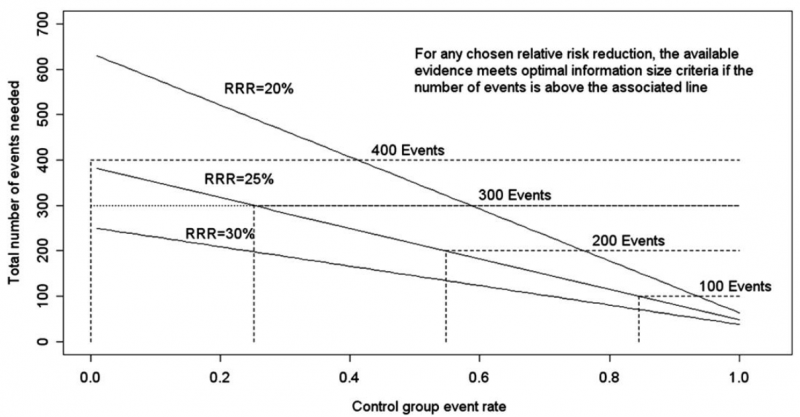
Power is, however, more closely related to number of events than to sample size. The figure presents the same relationships using total number of events across all studies in both treatment and control groups instead of total number of patients. Using the same choices as in the prior paragraph (control event rate 0.2 and RRR 25%), one requires approximately 325 events to meet OIS criteria.
Calculating the OIS for continuous variables requires specifying:
- probability of detecting a false effect – type I error (α; usually 0.05)
- probability of detecting a true effect – power (usually 80% [power = 1 – type II error; β; usually 0.20])
- realistic difference in means (Δ)
- appropriate standard deviation (SD) from one of the relevant studies (we suggest the median of the available trials or the rate from a dominating trial, if it exists).
For continuous variables we should downgrade when total population size is less than 400 (a threshold rule-of-thumb value; using the usual α and β, and an effect size of 0.2 SD, representing a small effect). In general an number of events of more then 400 guarantees the stability of a confidence interval.
5.5.5. Low event rates with large sample size: an exception to the need for OIS
In the criteria we have offered so far, our focus has been on relative effects. When event rates are very low, CIs around relative effects may be wide, but if sample sizes are sufficiently large, it is likely that prognostic balance has indeed been achieved, and rating down for imprecision becomes inappropriate. 
The decision regarding the magnitude of effect that would be important is a matter of judgment. When control rates are sufficiently low, CIs around relative effects can appear very wide, but CIs around absolute effects will nevertheless be narrow. Thus, although one would intuitively rate down for imprecision considering only the CI around the relative effect, consideration of the CI around the absolute effect may lead to an appropriate conclusion that precision is adequate. Note that the inference of unimportance requires a low incidence of events over the desirable duration of follow-up; short follow-up will generate a low incidence of events that may be misleading.
5.6. Publication bias
Publication bias is a systematic underestimate or an overestimate of the underlying beneficial or harmful effect due to the selective publication of studies. Publication bias arises when investigators fail to report studies they have undertaken (typically those that show no effect). Authors should suspect publication bias when available evidence comes from a number of small studies, most of which have been commercially funded.
A number of approaches based on the examination of the pattern of data are available to help assess publication bias. The most popular of these is the funnel plot. All, however, have substantial limitations and authors of reviews and guideline panels must often guess about the likelihood of publication bias. Again, there is no substitute for judgment.
Note that selective reporting of outcomes should be dealt with in the assessment of the individual studies.
Guideline panels or authors of systematic reviews should consider the extent to which they are uncertain about the magnitude of the effect due to selective publication of studies and they may downgrade the quality of evidence by one or even two levels. As there are no validated decision rules to do so it is important to provide a narrative justification of the final decision on this issue after consultation of the experts.
Trials registries are in principle compulsory now and can play a major role in detecting selective reporting.
5.7. Reasons to upgrade studies
Observational studies are by default considered low level of evidence. However, the level of evidence can be upgraded for a number of reasons. an important general remark on this issue: only studies with no threats to validity (not downgraded for any reason) can be upgraded. RCT evidence can in principle be upgraded, but GRADE considers this as rare and exceptional.
5.7.1. Large magnitude of effect
When methodologically strong observational studies yield large or very large and consistent estimates of the magnitude of a treatment or exposure effect, we may be confident about the results. In these situations, the weak study design is unlikely to explain all of the apparent benefit or harm, even though observational studies are likely to provide an overestimate of the true effect.
The larger the magnitude of effect, the stronger becomes the evidence. As a rule of thumb, the following criteria were proposed by GRADE:
- Large, i.e. RR >2 or <0.5 (based on consistent evidence from at least 2 studies, with no plausible confounders): upgrade 1 level
- Very large, i.e. RR >5 or <0.2 (based on direct evidence with no major threats to validity): upgrade 2 levels
5.7.2. All plausible confounders
On occasion, all plausible confounding from observational studies or randomized trials may be working to reduce the demonstrated effect or increase the effect if no effect was observed.
For example, if only sicker patients receive an experimental intervention or exposure, yet they still fare better, it is likely that the actual intervention or exposure effect in less sick patients is larger than the data suggest.
5.7.3. Dose-response gradient
The presence of a dose-response gradient may increase our confidence in the findings of observational studies and thereby increase the quality of evidence.
